(OroyFinanzas.com) – El protocolo Bitcoin utiliza el algoritmo ECDSA (Elliptic Curve Digital Signature Algorithm) para la creación de claves privadas y públicas. ECDSA es una variante del Digital Signature Algorithm (DSA) que utiliza la criptografía de curva elíptica (Elliptic curve cryptography – ECC) como variante de la criptografía asimétrica o de clave pública. En este artículo vamos a describir las principales características de la criptografía de curva elíptica y su aplicación en el protocolo Bitcoin.
La criptografía de curva elíptica puede ser más rápida y usar claves más cortas que los métodos antiguos — como RSA — al tiempo que proporcionan un nivel de seguridad superior.
Los primeros algoritmos de cifrado de clave pública se basaban en la factorización de números primos grandes, tal como describimos en nuestro artículo sobre las bases matemáticas del algoritmo RSA, pero estos ya no se consideran seguros cuando se cuándo utilizan claves cortas. La criptografía de curva elíptica con los actuales medios técnicos genera claves “intractable” en inglés, que traducido al español significa “difícil de resolver” pero no imposible, aunque con la tecnología actual tardaría miles de años.
¿Por qué utiliza el protocolo de Bitcoin criptografía de curva elíptica?
Uno de los problemas más importantes al que se tenía que enfrentar Satoshi Nakamoto cuando creó el protocolo Bitcoin fue la distribución de las claves públicas. Era importante poder utilizar claves públicas cortas, pero seguras que se pudieran compartir en códigos QR, imprimir en dispositivos físicos y compartir por teléfono si hacía falta.
La principal ventaja de la criptografía de curva elíptica es la posibilidad de crear claves más pequeñas, reduciendo así requisitos de almacenamiento y transmisión. Una clave basada en la criptografía de curva elíptica puede dar el mismo nivel de seguridad con un clave de 256 bits como un algoritmo RSA con una clave de 2048 bits.
El algoritmo ECDSA crea claves de 256 bits de longitud codificados con el sistema de numeración posicional Base58 de Bitcoin que da claves de 44 dígitos sin incluir el número de versión o dígitos de control. Una clave con RSA necesitaría de 350 dígitos.
La razón principal para utilizar criptografía de curva elíptica era pues facilitar el manejo de las direcciones públicas del protocolo Bitcoin.
Aun así, Satoshi Nakamoto decidió que los 44 dígitos eran demasiados para una dirección pública y decidió aplicar un proceso de funciones hash para la creación de las claves públicas que explicaremos en otro artículo. La clave pública ECDSA inicial acaba al final de ese proceso de hash en 160 bits que, incluyendo los datos de versión y los dígitos de control, tienen desde 27 a 34 dígitos. Por ejemplo como esta dirección pública: 1DZEazabbJqtr2uciLFNxvgm1GBuS5kaej
Bases matemáticas de la criptografía de curva elíptica
Los sistemas de criptografía asimétrica o de clave pública utilizan dos claves distintas: una de ellas es la clave pública, la otra es la clave privada. La posesión de la clave pública no proporciona información para determinar cuál es la clave privada. Este tipo de sistemas se basa en la dificultad de encontrar la solución a ciertos problemas matemáticos. Uno de estos problemas es el llamado logaritmo discreto. Encontrar el valor de b dada la ecuación a^b = c, cuando a y c son valores conocidos, puede ser un problema de complejidad exponencial para ciertos grupos finitos de gran tamaño.
En cambio, el problema inverso (la exponenciación discreta) puede ser evaluado eficientemente usando, por ejemplo, exponenciación binaria, la cual es ideal para su uso en la criptografía de clave pública en la que se necesita una clave privada segura y una clave pública que se pueda compartir con el resto del mundo derivada de la clave privada. Fuente de Wikipedia.
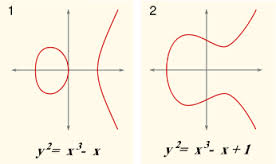
Una curva elíptica es una curva plana definida por una ecuación de la forma
y^2=x^3+ax+b
Donde a y b deben ser coeficientes no negativos. La curva elíptica es aquel lugar geométrico de los puntos del plano (x, y) en los cuales la diferencia entre la distancia de cualquier punto a cada uno de los focos es constante.
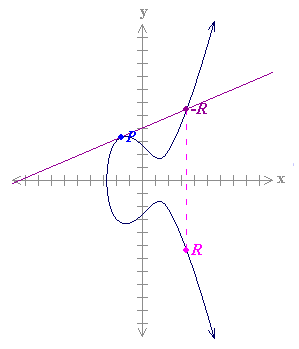
Con el conjunto de puntos G que forman la curva (por ejemplo, todas las soluciones de la ecuación más un punto O, llamado punto en el infinito) más una operación aditiva (la suma) se forma un grupo abeliano. Si las coordenadas x e y se escogen desde un cuerpo finito, entonces estamos en presencia de un grupo abeliano finito. El problema del logaritmo discreto sobre este conjunto de puntos (PLDCE) se cree que es más difícil de resolver que el correspondiente a los cuerpos finitos (PLD). De esta manera, las longitudes de claves en criptografía de curva elíptica pueden ser más cortas con un nivel de seguridad comparable.
David Perry explica los principios matemáticos de la criptografía de curva elíptica de una forma más accesible en su excelente artículo “Rubber Ducking Elliptic Curve Cryptography”
Base matemática del algoritmo ECDSA
Para una explicación matemática del algoritmo ECDSA y su aplicación en Bitcoin recomendamos la lectura de esta presentación de Akram El-Korashy:
Críticas a la criptografía de curva elíptica
En 2013 el New York Times revelo que la “Dual Elliptic Curve DeterministicRandom Bit Generation” (orDual_EC_DRBG – sec256r1) fue incluido por el NIST (National Institute of Standards, una agencia de la Administración de Tecnología del Departamento de Comercio de los Estados Unidos) influenciado por la NSA (National Security Agency – una agencia de inteligencia del Gobierno de los Estados Unidos) la cual había incluido deliberadamente una debilidad en el algoritmo.
Bitcoin utiliza el estándar de curva elíptica secp256k1. Esa no es la curva elíptica que supuestamente se ha visto comprometida por la NSA con el nombre de sec256r1.
En este video que analiza la criptografía de curva elíptica se explican algunos de estos aspectos: How did the NSA hack our emails?
En nuestro próximos artículos explicaremos la importancia de la longitud de las claves criptográficas, el algoritmo RIPEMD-160 y SHA-256.
© OroyFinanzas.com