(OroyFinanzas.com) – Para entender el funcionamiento del protocolo Bitcoin [1] y el potencial de la tecnología de la cadena de bloques (blockchain en inglés) [2] no hay atajos y solamente un entendimiento sólido de esta nueva tecnología permite valorar las posibles aplicaciones futuras. Antes de poder entender el funcionamiento de la blockchain, hay que entender una serie de conceptos criptográficos básicos que nos ayudarán a entender por qué Bitcoin es una criptomoneda [3]. En nuestro artículo de hoy explicaremos qué es una colisión (Collision en inglés) en el mundo de la criptografía y por qué utilizar funciones hash resistentes a colisión son fundamentales para el funcionamiento de Bitcoin. La resistencia a colisión es una de las tres propiedades que debe tener una funcion hash Bitcoin y explicaremos las otros dos propiedades (capacidad de ocultar o hiding, puzzles de búsqueda o puzzle friendliness) en otro artículo.
¿Qué significa el término colisión en el mundo de la criptografía?
Una colisión ocurre cuando dos valores de entrada diferentes generan el mismo resumen. Una función hash debe ser resistente a la colisión. El mismo Hash siempre será el resultado de los mismos datos (funciones deterministas), pero la modificación de la información, aunque sea un solo bit, dará como resultado un hash totalmente distinto.
La idea básica de un valor Hash (output en inglés) es que sirva como una representación compacta de la cadena de entrada (input en inglés). Este es un ejemplo de Wikipedia que muestra la importancia de que todos los datos de entradas sean iguales para llegar al mismo valor Hash y así ser deterministas.
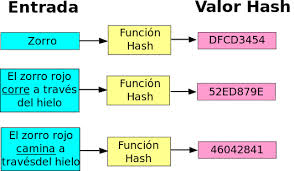
Fuente: Wikipedia [4] http://creativecommons.org/licenses/by-sa/3.0/deed.ese
Lo importante de un resumen criptográfico es que sea fácil crear el valor Hash, pero sea prácticamente imposible deducir el contenido de la entrada leyendo el valor Hash. Aunque sea muy fácil producir un Hash de una gran cantidad de datos cada resumen criptográfico es único.
Requisitos de una función Hash
En criptografía a este tipo de funciones que generan resúmenes se les denomina funciones hash. Son funciones que convierten una cantidad de bits de tamaño arbitrario a un conjunto reducido de bits denominado resumen, típicamente 128 ó 160 bits.
¿Cómo sabemos que una función hash es resistente a colisión y por tanto segura?
No lo sabemos. Sabemos que teóricamente todas las funciones hash no son resistentes a colisión, pero en la práctica podemos diferenciar entre dos tipos de funciones hash en relación a la colisión:
1) Funciones hash NO resistentes a colisión: Esto es para aquellas funciones hash para las que los investigadores y hackers de todo el mundo han intentado crear colisiones con éxito, por lo que no son seguras aunque lo fueran en el momento que fueran creadas, pero se quedaron obsoletas con la evolución tecnológica como en el ejemplo de la función hash MD5.
2) Funciones hash resistentes a colisión: Esto aplica a aquellas funciones hash donde investigadores y hackers de todo el mundo han intentado de forma empedernida crear colisiones, pero nadie lo ha conseguido. Estas funciones hash se consideran seguras por esa razón. La evolución tecnológica podría hacer que cualquiera de las funciones hash que hoy en día se consideran seguras no lo sean en el futuro, pero depende de los avances que se hagan en la capacidad de computación u otros métodos para atacar los algoritmos conocidos seguros.
¿Qué quiere decir que una función hash esté rota?
En criptografía se dice que un algoritmo criptográfico se rompe si por algún método se consigue reducir su fortaleza, es decir reducir por ejemplo su entropía de los 2^256 bits teóricos a tan sólo 2^255 por ejemplo. El hecho de que se encuentre una colisión no implica necesariamente que un algoritmo se haya roto, pues podría haber sido realizado mediante fuerza bruta, pero puede ser una causa.
Cuando se descubre una pareja de mensajes que generan el mismo resumen, la función hash ya no es resistente a colisiones y no ha sido por un ataque mediante fuerza se considera el algoritmo está roto. Esto es peor cuando se demuestran métodos para producir muchas colisiones de este tipo.
Dado que una utilidad importante de las funciones hash está en las firmas digitales, encontrar colisiones puede facilitar falsificar firmas digitales. Es decir, dos mensajes distintos que tengan un mismo resumen, tienen además la misma firma y un atacante puede reemplazar un mensaje por el otro. Un ejemplo de este ataque fue demostrado en 2008 por un grupo de investigadores en Amsterdam los cuales falsificaron un certificado raíz mediante el uso de un ataque de colisión contra el algoritmo MD5.
Ejemplo de por qué una función hash es segura frente la colisión aunque teóricamente sea imposible
Si seleccionamos 2^256+1 valores diferentes (o sea un número muy grande: 115 792 089 237 316 195 423 570 985 008 687 907 853 269 984 665 640 564 039 457 584 007 913 129 639 937) de entradas (input) con una salida (output) de 256 bits y generamos el hash de cada una de esas entradas y después comparamos todos los valores de salida generados por la función hash veremos que seguramente tengamos una colisión al haber elegido más valores de entrada (input) que valores de salida (output) porque alguno tendrá que generar una colisión. Con este metodo, está garantizado que habrá una colisión.
En cambio si seleccionamos valores de entrada aleatorios y generamos sus correspondientes valores hash de salida encontraremos una colisión mucho antes de haber comprobado los 2^256+1 valores posibles. Encontraremos comprobando tan solo 2^130 + 1 (1 361 129 467 683 753 853 853 498 429 727 072 845 825) valores una colisión con una probabilidad del 99,8% entre dos de esos valores. Explicaremos el por qué de esto en un artículo dedicado a la paradoja del cumpleaños (The birthday paradox).
Este método de detección de colisiones funciona para cualquier función hash. El problema que tiene este método es que tarda mucho mucho mucho tiempo. Para una función hash que genere 256 bits de valores de salida en el peor de los casos tendríamos que comparar 2^256 + 1 para encontrar una colisión, pero de media “solo” tardaríamos 2^128 (340 282 366 920 938 463 463 374 607 431 768 211 456 valores). Este número es muy grande y si tuviéramos un ordenador que pudiera calcular 10.000 hash por segundo tardaría un octillón de años (10^27 = 1 000 000 000 000 000 000 000 000 000) para calcular los 2^128 hash de salida. Una forma sencilla para imaginarse esto si utilizamos todos los ordenadores jamás fabricados por la humanidad y estuvieran calculando esos valores hash desde el principio del universo hasta el presente la probabilidad de que encontráramos una colisión seguiría siendo infinitamente baja.
Estos ataques de fuerza bruta para las funciones hash modernas, por tanto, no son muy útiles y obviamente las agencias de seguridad de información como la NSA y otras agencias intentan utilizar otros métodos para crear colisiones. Por eso es fundamental que el algoritmo de cualquier función hash sea público porque al estar expuesto al escrutinio de científicos, investigadores y hackers la probabilidad de que nadie de ellos encuentre una colisión los hace más seguros.
Resistencia a pre-imagen – Colisiones
En criptografía, a las entradas que dan el mismo resumen se les denomina pre-imágenes. Cuando la salida es reducida y la entrada puede ser muy grande, existen muchas entradas diferentes que darán el mismo resumen y por tanto una colisión. Una buena función hash debe ser resistente a pre-imagen, es decir, debe ser computacionalmente inviable que un atacante deduzca fácilmente, o sea que tenga que tardar cientos o miles de años con recursos computacionales importantísimos, las diferentes entradas que producen una misma salida. Esto se llama resistente a colisión.
Resistente a segunda pre-imagen – Colisiones
Pero no sólo eso, sino que además deben ser resistentes a ataques de segunda pre-imagen, es decir, debe ser computacionalmente inabordable que, partiendo de un mensaje, sea posible encontrar otro que sea modificación del primero y cuyos resúmenes coincidan.
Por tanto, si una función hash es resistente a una segunda pre-imagen entonces la función unidireccional [5] lo seguirá siendo incluso aunque se conozca la relación de que un mensaje deriva en un resumen concreto.
Por ejemplo, la idea de generar resúmenes de ficheros es muy útil criptográficamente para firmar ficheros o mensajes, y por tanto, garantizar la autoría de ese contenido. En la práctica, por eficiencia en lugar de aplicar la firma digital al mensaje completo se realiza sólo al resumen generado. Como el atacante no es capaz de encontrar diferentes mensajes que den el mismo resumen, entonces firmar el resumen es tan válido como firmar el documento entero.
La utilidad de que las funciones hash sean resistentes a segunda pre-imagen facilita firmas en documentos de tamaño arbitrario.
Ejemplo de colisión en criptografía
Supongamos que contratamos a un amigo para hacer un trabajo y firmamos un documento en el que dice que le pagaré 5.000 Euros. Misteriosamente, al mes siguiente, nuestro amigo vuelve con el contrato firmado por nosotros en el que se indica que le pagaremos 50.000 Euros por ese mismo trabajo. Ahora la pregunta: ¿cómo es esto posible?
Sólo sería posible si el contrato original y el modificado tienen el mismo resumen. Pero, ¿no se suponía que un atacante no puede hacer esto si la función hash implementa las medidas oportunas?
Si nuestro amigo ha generado los dos contratos, antes de que los firmáramos, y ambos tienen el mismo resumen sería posible esta situación. Lo que tenemos que evitar es que sea computacionalmente factible calcular dos mensajes que generen el mismo resumen (es decir, una colisión) para la misma función hash.
Ejemplo del uso de la criptografía resistente a colisión: Descargas seguras de Software
Un uso práctico de todos los días para las funciones hash resistentes a colisión es la descarga segura de software. Si conocemos el valor hash de un fichero seguro podemos descargar este software de cualquier sitio y comparar el hash de ese software que descargamos con el hash del software seguro. Si coinciden los valores hash, el software es seguro para su uso. Si los valores hash no coinciden puede significar que alguien haya introducido un virus o que en la transmisión se haya modificado ficheros o haya habido otro error. Con este método podemos crear valores hash únicos para software pesado y ficheros de todo tipo y compartirlos de forma segura. Muchas páginas web que comparten programas de código abierto [6] aseguran así que se puedan descargar esos programas con total seguridad.
Consideraciones prácticas: Procedimientos, criptoanálisis y consecuencias
En la práctica criptográfica se reutiliza mucho del conocimiento existente en la construcción de algoritmos criptográficos y, en particular, de la construcción de algoritmos de cifrado en bloque. Por ejemplo, aquí también se persiguen que entradas muy parecidas a nivel de bits generen salidas completamente diferentes y no correlacionadas. Por ejemplo, en cifradores de bloque de n vueltas, modificar un solo bit puede hacer que en una pasada del algoritmo cambien el 50% de los bits resultantes.
Sin embargo, hay una gran diferencia entre funciones hash [7] y funciones de cifrado como la secreta o de clave pública. El objetivo de las primeras no es proteger un secreto o la confidencialidad. Además lo habitual es que las funciones hash no necesiten del uso de claves secretas. Esta es una de las características que hacen que su diseño sea más difícil. No obstante, sí comparten la filosofía de que los algoritmos actuales son públicos y por tanto el atacante intentará vencer al algoritmo por este hecho.
De hecho, el diseño de funciones hash se ha ido renovando gracias a las propuestas de ataque de criptoanalistas. Por ejemplo, los algoritmos estándar de funciones hash desarrollados y utilizados desde la década de los 90, como MD5 o SHA-1, hoy en día o están rotos o significativamente amenazados. Bitcoin no se basa en ninguno de ellos porque utiliza SHA-256 [8] como función hash principal y ECDSA [9] junto a RIPEMD-160 [10] en el proceso de creación de direcciones [11]. SHA-256, una función hash muy conocida, es utilizada en combinación con RIPEMD-160 porque el uso del protocolo Bitcoin de una dirección pública podría crear riesgos de seguridad por interactuaciones imprevistas entre RIPEMD-160 y ECDSA. ECDSA es el algoritmo de creación de un par de claves privada y pública de Bitcoin. Se asume que la interposición de SHA-256 entre ECDSA y RIPEMD-160 hace casi imposible encontrar colisiones de una dirección pública Bitcoin.
Fuente: Bitcoin and Cryptocurrency Technologies de Arvind Narayanan y otros profesores de Princeton [12] e Intypedia [13]
© OroyFinanzas.com